[미적분학]
벡터미적분 : 응용편~ 평면에서의 발산 정리 (1편)
Calculus: Vector Calculus (Deepening problem~ Divergence Theorem in a Plane -1-)
안녕하세요, Hub1 입니다.
개념과 기본 유형의 문제들을 모두 마치고, 이번에는 심화 과정을 하나 언급하려 합니다.
바로,
"평면에서의 발산 정리"에 대해 다루어 보고자 합니다.
이것의 다른 이름으로는,
"곡선의 유량"="곡선의 유출량(Flux)"="법선방향의 일(Work)" 이라고도 합니다.
해당 정리에 대해 명확한 명칭은 없는 것으로 알고 있습니다.
따라서 위에서 언급한 것들은 모두 제가 배운 것, 또는 직접 명명한 것입니다.
참고로 해당 내용은 난이도가 높기 때문에, 총 3부작으로 나누어서 작성할 것입니다.
오늘은 1부에 대해 시작하겠습니다.
일반적으로 알고 있는
*(공간에서의) 발산 정리

(폐곡면S로 둘러싸인 단순연결영역E에서, 벡터장F=<P,Q,R>의 성분 P,Q,R이 연속인 일계편도함수를 가질 때)
사실은 이것은 "평면에서의 발산 정리"를 "한 차원"높인 것 입니다.
*평면에서의 발산 정리:

(양의 방향의 폐곡선C로 둘러싸인 영역D에서, 벡터장 F=<P,Q>의 성분 P,Q가 연속인 일계편도함수를 가질 때)
평면의 발산정리에 대해 증명해보겠습니다.
(증명)

위와 같은 단순폐곡선C가 xy평면상에 있다고 합시다.
이때, 이 곡선을 매개변수로 표현하면 r(t)=<x(t),y(t)> 라고 할수 있습니다.

이제 이 곡선의 접선벡터는 위와 같이 표현이 가능합니다.
접선벡터의 특징: 곡선의 진행방향과 항상 같은 방향의 벡터.
(접선벡터는 곡선C의 매개변수인 r(t)를 t에 관해 미분하면 됩니다.)

이제는 위에 표시한대로, 단위법선벡터
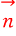
를 알아봅시다.

로 표현합니다.
단위법선벡터의 특징: 곡선의 진행방향과 수직한 방향의 벡터.
(지금 표시한 단위법선벡터는 곡선의 바깥 방향으로 하였습니다.)
(또한, 구하는 방법의 증명은 생략. 외워두면 유용)

이제 처음으로 돌아와서, 이 곡선C를 어떠한 벡터장이 존재하는 공간에 띄워봅시다(놓아봅시다).
그렇다면 이 벡터장F가 곡선C에 대해 일(Work)을 해주겠죠?
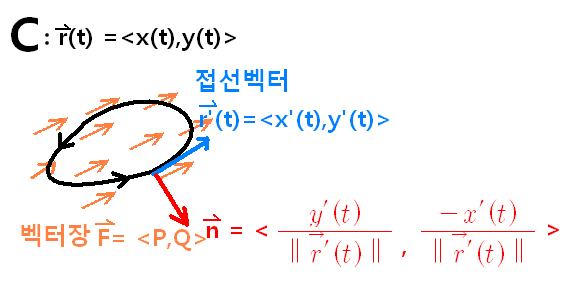
앞에서 배운 개념들을 모두 합쳐 하나로 표현한 것입니다.
다시 말해, 벡터장F가 곡선C에 대해 일(Work)을 하긴 하는데,
우리는 2가지 방향(접선 방향과 법선방향)에 초점을 두고 접근하겠습니다.




댓글