[미적분학]
벡터미적분 : 응용편~ 평면에서의 발산 정리 (2편)
Calculus: Vector Calculus (Deepening problem~ Divergence Theorem in a Plane -2-)
지난 시간에 평면에서의 발산정리에 대해 1편을 보았습니다.
이제 2편을 이어서 나가겠습니다.
(1부에 이어서 계속 증명)
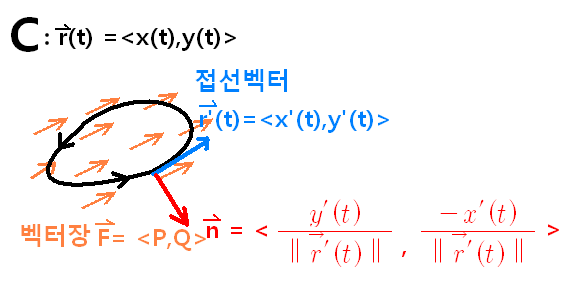
1부 마지막에서 배운 개념들을 모두 합쳐 하나로 표현한 것입니다. [벡터장에 존재하는 곡선C]
다시 말해, 벡터장F가 곡선C에 대해 일(Work)을 하긴 하는데,
우리는 2가지 방향(접선 방향과 법선방향)에 초점을 두고 접근하겠습니다.
여기서 필자는,
벡터장F가 곡선C에 접선 방향으로의 한 일을

벡터장F가 곡선C에 법선 방향으로의 한 일을

으로 표현하겠습니다.
1. 접선 방향에 대한 일(Work)

이것은 그동안 일반적으로 우리가 자주 써왔던
벡터장에서의 선적분

을 의미합니다.
즉, 우리가 그동안 했던 벡터장에서의 선적분은 사실..
곡선C에 대해 벡터장F가 접선방향으로의 한 일(Work)을 구한 것입니다.
따라서 접선 방향에 대한 일은

로 표현합니다.
또한, 만약 곡선C가 폐곡선이라면, Green정리(그린 정리)를 사용하여 아래와 같이 가능합니다.
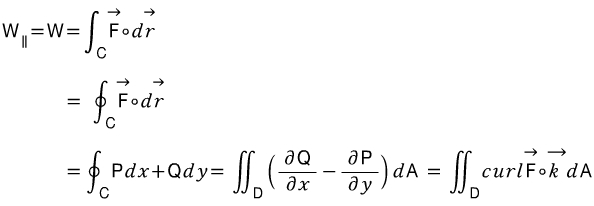
2. 법선 방향에 대한 일(Work)
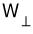
이번 포스팅의 가장 주된 목적이 바로 이것 '법선방향에 대한 일(Work)' 때문입니다.
우리가 그동안 해온 것은.. 접선 방향에 대한 일(Work)이고 이것을 선적분 표현하는 방법에는 꽤나 익숙한 편입니다.
그렇다면, 이 법선방향에 대한 일은 어떤 방식으로 선적분 표현을 할까요?
바로 아래와 같습니다.
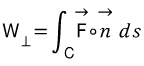
(물리적 해석: 벡터장F(힘)과 단위법선벡터를 서로 내적하면, 법선방향의 벡터장F(힘) 성분을 뽑아낼 수 있다.
이렇게 뽑아낸 법선방향의 힘 성분을 곡선에 대해 적분하면 법선방향의 총 일(work)를 의미한다.)
이것을 좀 더 수식으로 표현하겠습니다.
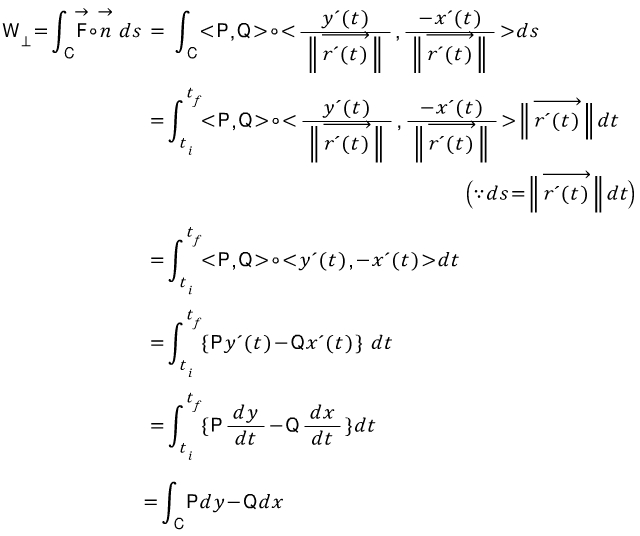
식이 깔끔해졌죠?
즉, 정리하자면

가 된다는 것입니다.
(매우 보기 편한 식이 되네요)
이제 여기서 추가적인 조건을 넣겠습니다.
"C가 단순폐곡선"이라는 조건을 추가하면, 역시나 Green정리를 쓸 수 있습니다.

이제 "평면에서의 발산정리"가 보이나요?
최종적으로 벡터장F가 곡선C에서 법선 방향에 대해 한 일(Work)은
Flux (유출량)과 "같은 의미"로 쓰인다는 것입니다. (그래서 처음에 n을 바깥으로 빠져나가는 방향으로 잡음)
(곡선의 유량/곡선의 유출량)
발산정리가 사실은, 평면에서의 Green 정리에서 유래됐다는 점도 알 수 가 있네요.




댓글